
エクセルを用いて確率0.95からt値を求めるには,一般的には(ここ,を参照),
両側:T.INV.2T(確率,自由度)もしくは,T.INV(1-確率/2,自由度)
片側:T.INV(1-確率,自由度)
を用いるようです.
これを小数点を含む自由度で計算すると,
| 自由度 | 0.05 |
| 2 | 4.30265 |
| 2.1 | 4.30265 |
| 2.2 | 4.30265 |
| 2.3 | 4.30265 |
| 2.4 | 4.30265 |
| 2.5 | 4.30265 |
| 2.6 | 4.30265 |
| 2.7 | 4.30265 |
| 2.8 | 4.30265 |
| 2.9 | 4.30265 |
| 3 | 3.18245 |
| 3.1 | 3.18245 |
| 3.2 | 3.18245 |
| 3.3 | 3.18245 |
| 3.4 | 3.18245 |
| 3.5 | 3.18245 |
| 3.6 | 3.18245 |
| 3.7 | 3.18245 |
| 3.8 | 3.18245 |
| 3.9 | 3.18245 |
| 4 | 2.77645 |

となり,階段状に推移していることになります.詳しく見てみると,
切り下げ
していることがわかります.つまり,厳しめの値を採用していることになります.
t分布自体は,
\(\Large \displaystyle f(t) = \frac{ \Gamma (\frac{n}{2}) }{ \sqrt{(n-1) \pi} \ \Gamma ( \frac{n-1}{2})} \left( 1 + \frac{t^2}{n-1} \right)^{- \frac{n}{2}}\)
となりますが,両側0.95の自由度を計算してみると,
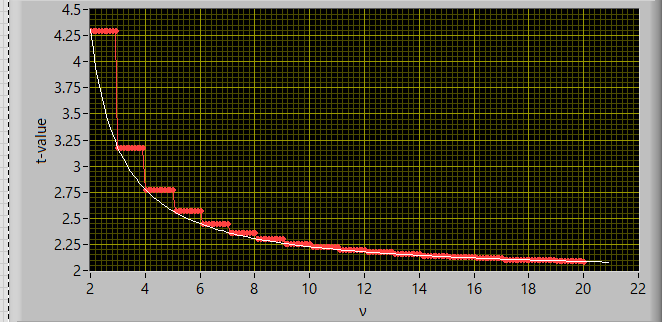
と連続関数になるので,計算可能なことは可能ですね.
つぎはいよいよ,検定,です.